ケーキを取り分けるイメージで、文系的に分数の割り算を理解する

1 分数の割り算も感覚的に理解できる

分数の割り算も感覚的に理解できる

小学校の算数で多くの子がつまずくポイントは、3年生、4年生で教わる「分数」の計算です。ここで分数という概念があまり理解できず、算数に苦手意識をもってしまう子供がどうしても多い。

分数が出てきて急に算数が難しくなるのは実生活であまり分数を使う機会がなく、低学年でやってきた自然数（１、２、３…）の計算と異なり、感覚的に理解しづらい点です。

とくに文系能力が優れた子供は、数式の内容を現実のモノに置き換え（例えば数字をリンゴに置き換えたりしながら）、自分で具体的なイメージを作り問題を解いていたりします。

なので「100円持っていて50円使うと、残りは50円」というのはすんなり理解できるのですが、「100円のうち1/2を使う」となると経験則的理解ができず、一気に混乱してしまい算数が苦手になってしまいます。

文系的な思考で分数の割り算はこなせる

まあ分数の概念を理解できてなくても、計算の方法（逆数を掛ける）さえ覚えれば問題は解けるのですが、どうしても応用が利かなくなる。特に文章問題などで自分で式を作るときに、苦労してしまいます。

ぶっちゃけ小学校で扱う分数の計算はイメージ（感覚）で理解できる範囲です。なのでこの段階で苦手意識を持ってしまうのは非常にもったいない。

分数に対する苦手意識を少しでも払拭できるよう、文系的な思考で十分解けるという話をしてみようと思います。

”１”といっても色々ある

分数の問題を感覚的に理解するには、数式を具体的にイメージ化することが必要です。そのために押さえておかなければいけないポイントは、同じ分数でも基準によって意味が変化する点です。

というか分数に限ったことでなく数学の前提条件なのですが、「１」の意味は定義によって変化することを認識することが分数の計算においては特に大切になります。

数式上では常に「１」は「１」でしかありませんが、文章問題では「１」の意味が変化します。例えば”コップ１杯の水”と言ってもコップの大きさで水の量は違います。

マグカップとワイングラスでは同じ1杯でも、量が変わってくるのは当然です。

あたりまえですが、この基準は何か（１が何を意味しているのか）ということを意識するだけで、一気にイメージが作りやすくなります。

基準が変わると、分数の意味が変わる

ちょっと抽象的な話でわかりにくくなったので、簡単な例題を使って説明します。

問１　水槽に水が1/2リットル入っています。そこへ1/2リットルの水を足しました。水は合計何リットルでしょう。

問２　水槽に水が半分（1/2）入っています。水槽の容量は4リットルです。水は何リットル入っているでしょう。

まずは計算式を書きます。

問１　1/2 ＋ 1/2＝ 1　答え　1リットル

※単位をつけると　1/2（リットル）+1/2（リットル）=１（リットル）

問２　4 × 1/2 ＝ 2　答え　2リットル

※単位をつけてると　4（リットル）×　1/2 ＝ 2（リットル）

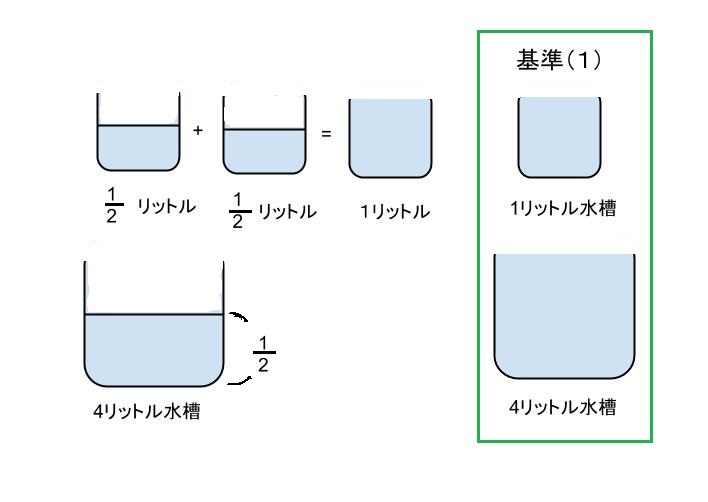
問１の文章中であらわす1/2はズバリ1リットルに対しての半分の意味なので0.5リットルです。比べて問2の文章中の1/2は4リットルの水槽に対しての1/2なので、結果2リットルを表します。

数式上は全く同じ1/2ですが、文章問題上に示される1/2の意味は異なることが解かります。大事なのは”基準によって数字の意味が変わる”ことを意識することです。

当たり前のことなんですが、ここを意識してておくと国語的、文系的に数式のイメージが作りやすくなり、問題を解く場合にもミスが減ります。

分数の割り算はケーキを取り分けるイメージで

前置きが長くなりましたが、分数の割り算を文系的イメージで理解するという本題に入ります。基本的な分数の割り算を具体的にイメージ化していきます。

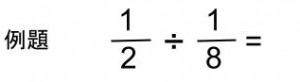
割り算を具体的なイメージとして捉える為、ケーキを取り分けるイメージでビジュアル化していきます。

1.まずは「１」の基準を明確にしておきます。ホールケーキ丸ごと一個を「１」とイメージします。

2.数式をそのままケーキに当てはめます。ホールケーキ1/2サイズをイメージして、そのケーキを1/8サイズで切り分ける（割り算をする）イメージです。

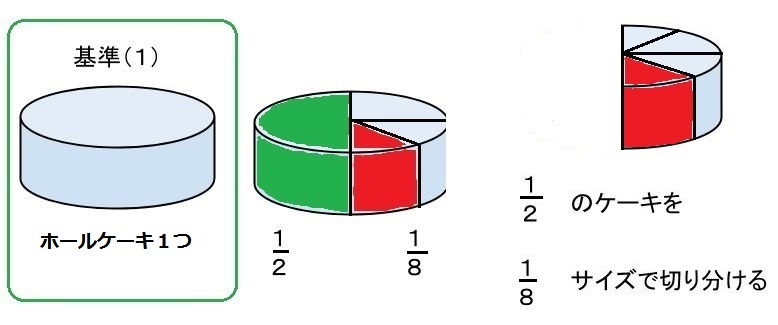
数学的に1/8の逆数8をかけて1/2×8=4と考えなくても、文系的な創造力で十分に問題が解けます。逆数を掛けるという公式を忘れても、感覚だけで対処できるところがポイントです。

ちなみにわかりやすく上記の数式を文章問題に起こすと

お父さんは花子さんの誕生日にホールケーキを一つ買ってきました。ですが花子さんはダイエット中だったのでホールケーキの1/2だけを食べてあとは冷蔵庫に入れておきました。

次の日、花子さんの家に高校時代のクラスメートがやって来ました。花子さんは20年ぶりの再会のお祝いに、昨日のホールケーキの残りを1/8サイズに切ってみんなに出してあげることにしました。

さて花子さんは何人分のケーキを用意することができたでしょうか。

といった感じになります。